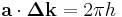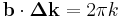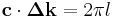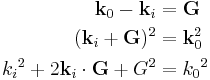Laue equations

In crystallography, the Laue equations give three conditions for incident waves to be diffracted by a crystal lattice. They are named after physicist Max von Laue (1879 — 1960). They reduce to the Bragg law.

Equations

Take 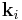\mathbf{k}_i to be the wavevector for the incoming (incident) beam and 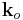\mathbf{k}_o to be the wavevector for the outgoing (diffracted) beam. 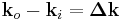\mathbf{k}_o - \mathbf{k}_i = \mathbf{\Delta k} is the scattering vector and measures the change between the two wavevectors.

Take 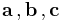\mathbf{a}\, ,\mathbf{b}\, ,\mathbf{c} to be the primitive vectors of the crystal lattice. The three Laue conditions for the scattering vector, or the Laue equations, for integer values of a reflection's reciprocal lattice indices (h,k,l) are as follows:

\mathbf{a}\cdot\mathbf{\Delta k}=2\pi h
\mathbf{b}\cdot\mathbf{\Delta k}=2\pi k
\mathbf{c}\cdot\mathbf{\Delta k}=2\pi l

These conditions say that the scattering vector must be oriented in a specific direction in relation to the primitive vectors of the crystal lattice.

Relation to Bragg Law

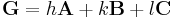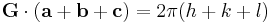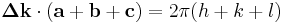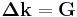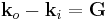If  \mathbf{G}=h\mathbf{A}%2Bk\mathbf{B}%2Bl\mathbf{C}  is the reciprocal lattice vector, we know  \mathbf{G}\cdot (\mathbf{a}%2B\mathbf{b}%2B\mathbf{c})=2\pi (h%2Bk%2Bl). The Laue equations specify  \mathbf{\Delta k}\cdot (\mathbf{a}%2B\mathbf{b}%2B\mathbf{c})=2\pi (h%2Bk%2Bl). Whence we have  \mathbf{\Delta k}=\mathbf{G}  or  \mathbf{k}_o - \mathbf{k}_i = \mathbf{G}.

From this we get the diffraction condition:

\begin{align} \mathbf{k}_0 - \mathbf{k}_i &= \mathbf{G}\\ (\mathbf{k}_i %2B \mathbf{G})^2 &= \mathbf{k}_0^2\\ {k_i}^2 %2B 2\mathbf{k}_i\cdot\mathbf{G} %2B G^2 &= {k_0}^2 \end{align}

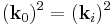Since : (\mathbf{k}_0)^2=(\mathbf{k}_i)^2 (considering elastic scattering):

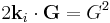2\mathbf{k}_i\cdot\mathbf{G}=G^2.

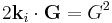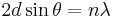The diffraction condition  \;2\mathbf{k}_i\cdot\mathbf{G}=G^2  reduces to the Bragg law  \;2d\sin\theta =n\lambda.

References